Article rédigé par Monsieur P. Trehin, chargé de cours à l’université de Nice.
Cet article présente de manière simplifiée une méthode puissante d’analyse de distributions statistiques de populations spécifiques en fonction de la taille des différentes entités qui les composent. J’ai utilisé et perfectionné cette méthode pendant ma carrière à IBM, pour des analyses de structures de marchés dans le domaine des produits informatiques ou de réseaux informatiques ainsi que de marchés pour des centraux téléphoniques privés, domaines dans lesquels la taille des établissements et des entreprises ainsi que leur distribution statistique permettait une modélisation prévisionnelle relativement précise.
En effet : Ce type de distributions est remarquablement stable, dans le temps et dans l’espace selon les divers secteurs géographiques et est connu sous le nom de » distributions de Pareto », du nom de Vilfredo Pareto, célèbre économiste/sociologue Suisse. Il a découvert qu’au-dessus d’une certaine taille, la répartition cumulative du revenu des ménages, une fois tracée sur un graphique Log-Log, forme une ligne presque droite. La théorie a été depuis affinée, la méthode n’en est que plus efficace.
L’échelle Log-Log est généralement employée dans l’analyse de la distribution reliant le nombre de personnes à leur niveau de revenu, mais est également employée pour analyser les distributions statistiques suivantes : nombre d’établissements industriels et commerciaux, le nombre d’entreprises industrielles et commerciales, de Centraux téléphoniques privés, etc. par rapport à leurs tailles respectives exprimées par des mesures appropriées aux entités analysées: nombre d’employés dans les établissements ou les entreprises, : chiffre d’affaire annuel dégagé par les établissements ou les entreprises ; nombre de postes de téléphones reliés aux centraux téléphoniques privés, etc.). Ces distributions suivent, en général, une « Loi de Pareto » encore appelée « Distribution de Pareto ».
Nous proposerons une variation à la technique classique d’analyse de la distribution de Pareto qui donne des résultats plus précis et sur un plus grand domaine de taille que la méthode de Pareto pure.
Rappels
Pareto a découvert vers 1875 la distribution qui porte maintenant son nom en étudiant la répartition des revenus des familles en Suisse. Il était communément admis qu’il y a plus de familles avec un bas revenu que de familles avec un revenu élevé et l’observation factuelle confirmait cette idée. Ce qui était alors encore inconnu c’est que ces distributions ont une forme très régulière.
Pareto dans son analyse des répartitions du revenu des ménages des familles s’est retrouvé devant un problème de représentation graphique.. En effet, étant donné l’étendue des écarts de revenus d’un côté et l’étendue encore plus large des populations regroupées dans les diverses classes de niveau de revenu (Se comptant en millions dans les classes à bas revenu, et en centaines, voir dizaines pour les classes à revenu très élevés), Pareto a dû employer le papier graphique Log-Log afin de condenser les échelles et de pouvoir représenter toutes les valeurs sur un même diagramme.
Il a alors remarqué que non seulement le nombre de familles ayant des revenus bas était effectivement et significativement plus élevé bas que le nombre de familles avec des revenus élevés, mais en outre, que la distribution suivait une ligne droite sur un graphique Log-Log. Plusieurs autres études ultérieures, à d’autres époques, dans d’autres pays, ont conduit à un résultat empirique surprenant : toutes ces distributions suivaient une loi statistique identique quelque soient les pays ou les époques soumises à analyses.
Pareto avait utilisé des effectifs cumulés dans son analyse des distributions de revenus. C’est sur ces effectifs cumulés que le tracé d’un une courbe cumulative de distribution a fait apparaître la linéarité de la distribution sur une échèle log log.
La recherche empirique a prouvé que les caractéristiques de la distribution suivent la même loi, sans utiliser des effectifs de classes cumulés. Le reste de cet article se concentrera sur cette dernière situation de distributions non cumulatives des effectifs de chaque classe.
Dans la figure ci-dessous, on a une visualisation de ce que nous venons de décrire.
Figure 1 : Distribution des revenus en fonction de la taille du revenu
Log du Nombre de familles
Avec un revenu X

La ligne droite, en échelle logarithmique, sur une partie du graphique se prête aux calculs mathématiques faciles.
Y = A X + B
Dans laquelle grand X est le logarithme du niveau de revenu petit x, et grand Y est le logarithme du nombre de personnes ayant un revenu petit x ce qui évite la notation lourde :
Log( y ) = A log (x) + B
Après transformation, comme la coefficient A est négatif, l’équation arithmétique correspondante est une hyperbole :

Cette forme de droite est très reconnaissable et permet d’orienter les recherches ultérieures. Elle permet aussi l’interpolation de valeurs intermédiaires absentes, l’évaluation de valeurs pour des limites de classe de taille différentes, etc.
La distribution de Pareto est cependant en échec pour fournir un bon ajustement à l’extrémité inférieure du continuum de taille, où une ligne droite ne s’adapte plus aux données observées. En fait Pareto lui-même avait exprimé l’idée que son observation n’était valide que seulement au-dessus d’un revenu minimum X0. Le même phénomène se retrouve dans les autres distributions ; le classes de taille inférieures ne suivent plus une ligne droite en dessous d’une certaine taille
L’analyse empirique, avec l’aide de calculs informatisés, m’a conduit à utiliser un ajustement du second degré sur les effectifs de classes normalisés plutôt qu’un ajustement linéaire. Je me suis alors aperçu que l’ajustement avec une parabole plutôt qu’une ligne droite, permettait de prolonger vers les plus basses classes de taille un ajustement très précis de la courbe à la population analysée1.
Des recherches bibliographiques m’ont permis de vérifier la validité de cette approche en effet certains statisticiens avaient déjà commencé à employer des distributions plus sophistiquées que la distribution de Pareto : la distribution « log-normale ». Une fois transformée par une échelle Log-Log, la technique d’ajustement emploie une équation parabolique au lieu d’une équation linéaire. Mais compte tenu de la plus grande complexité des calculs de régression parabolique par rapport à ceux de régressions linéaires, il semble qu’ils aient assez peu réutilisé cette technique d’ajustement malgré sa meilleure adéquation aux populations analysées. Toutefois j’avais trouvé une ou deux publications où ces chercheurs concluaient qu’à partir d’une certaine taille les distributions de Pareto et les distributions log normales devenaient insignifiantes au niveau statistique.
Mais le résultat le plus intéressant dans la pratique est de permettre une extrapolation plus précise dans les tailles basses de la distribution, voir note N°1
Y = A X²+ B X + C
Dans laquelle grand X est le logarithme du niveau de revenu petit x
Et grand Y est le logarithme du nombre de personnes ayant un revenu petit x
L’analyse empirique prouve que cet ajustement avec une régression du second degré donne de très bons résultats et qu’au-dessus d’une certaine taille elle est statistiquement indiscernable de la distribution originale de Pareto. Un calcul mathématique simple prouve qu’après transformation et retour à une échelle arithmétique, l’équation du second degré devient celle de la distribution Log-Normale. Dans le reste de cet article j’emploierai le terme de distribution de Pareto comme nom générique puisque ce terme est relativement mieux connu, tout en gardant à l’esprit que le véritable nom de la distribution est Log-Normale.
Domaines d’applicabilité des distributions de Pareto
L’analyse ultérieure des distributions statistiques a démontré que les distributions de Pareto étaient en effet très communes dans divers champs d’application :
- Distribution des entreprises par taille en nombre d’employés
- Entreprises par taille de revenu annuel
- Distribution des établissements distribution par taille en nombre d’employés
- Distribution des centraux téléphoniques privés par taille en nombre de postes téléphoniques installés
- Ménages en fonction de leurs revenus annuels
- Distribution des Ordinateurs par taille de prix
– par capacité de la mémoire
– par puissance de calcul - etc.
Voici un exemple d’application de cette loi statistique aux USA : le nombre d’établissements en fonction de leurs tailles exprimée en nombre de personnes employées par ces établissements.

En vingt ans, malgré la crise pétrolière de 1973/1975, la distribution est restée extrêmement stable.
Autre exemple comparaison entre la distribution des établissements par taille d’employés aux USA et en Europe Midle East Africa (EMEA)1 :

(EMEA abbreviation Europe Middle East Africa)
On notera dans cet exemple que la méthode permet de comparer des distributions alors même que les limites de classes étaient différentes en Europe et aux USA.
La stabilité remarquable de toutes ces distributions, dans le temps mais aussi selon la région géographique fait de cette technique statistique un puissant instrument d’analyse et de prévision.
Quand on doit-on rechercher une distribution de Pareto ?
Les distributions de Pareto ont toutes en commun les caractéristiques suivantes :
Elles dénombrent un ensemble d’entités par rapport à une mesure de leurs tailles exprimées selon diverses modalités :
- Nombre des entreprises ayant une certaine taille en nombre d’employés, en revenu annuel, en consommation d’énergie, etc.
- Nombre des personnes ayant un certain niveau de revenus
- Nombre des réseaux informatiques ayant un certain nombre de postes de travail connectés
La taille a une limite supérieure ouverte (au moins théoriquement)
- Nombre d’employés dans une entreprise, au moins en théorie, peut se prolonger indéfiniment
- La puissance d’un ordinateur, de même
- Nombre de postes de travail connectés dans un réseau aussi
La mesure de taille est homogène
- L’unité qui mesure la taille est la même pour l’ensemble de la population
- Ordinateur : la taille est mesurée en puissance du processeur dans toute l’analyse, si l’on a choisi une autre mesure, taille mémoire centrale par exemple, on s’y tient pour toute l’analyse.
- Nombre de postes de travail connectés dans un réseau est utilisée comme mesure de la taille pour tous les réseaux.
On travaille sur de grandes Populations
Il y a évidemment un certain degré d’expertise impliqué dans la décision d’employer une distribution de Pareto, basée sur l’expérience d’avoir fait face à de nombreux cas dans des domaines variés.
Tester l’ajustement à la distribution de Pareto
Rappelons nous que nous avons pour le moment seulement fait l’hypothèse que la distribution que nous analysons est de type « Pareto ».
La première étape consiste à tracer les données sur une échelle Log-Log pour vérifier visuellement que la courbe suit le modèle parabolique attendu. C’est un exercice de tracé très simple qui peut être fait en utilisant soit un papier à échelle Log-Log ou plus facilement, de nos jours, en choisissant l’échelle Log-Log pour l’axe des X et des Y dans le programme graphique de l’ordinateur.
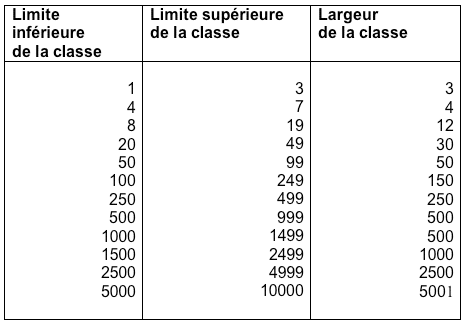
Il y a cependant des pièges à éviter. Les données nous parviennent, en général, déjà groupées par classes de taille : (5 à 9) (10 à 19) (20 à 49) (50 à 99). Les frontières de classes de taille sont en général arbitraires et fournissent rarement des intervalles égaux.
On doit donc employer la méthode classique du tracé d’histogrammes normalisé, celle-ci consiste à employer le tracé normalisé des distributions statistiques et à déterminer le centre de classe pour permettre de tracer une courbe.
* La hauteur de la barre de l’histogramme est calculée en divisant la quantité mesurée appartenant à chaque classe de taille par la largeur de la classe de taille correspondante.
Cela permet une représentation normalisée des quantités, quelle que soient les largeurs des tailles de classes choisies.
* Le centre de la classe de taille n’est pas la moyenne arithmétique des extrémités mais la moyenne géométrique. C’est à dire la racine carrée du produit de la limite inférieure par la limite plus élevée.
L’abscisse du point tracé doit prendre en compte le fait que la taille moyenne dans chaque classe de taille est biaisée vers l’extrémité basse. Quand c’est possible, il vaut mieux utiliser la taille moyenne réelle. Quand cette moyenne réelle n’est pas disponible l’analyse empirique a prouvé qu’on peut employer la moyenne géométrique des limites de la classe de taille comme approximation acceptable. On notera que sur le tracé en Log-Log, ce point semble être au milieu de la classe, cela est dû à l’échelle logarithmique.
J’ai tracé volontairement le graphique ci-dessous de façon simplifiée pour que les éléments décrits ci-dessus puissent être facilement identifiés
Log du nombre d’entreprises Appartenant à la classe de taille X

L’essai visuel confirmera immédiatement ou infirmera l’hypothèse faite que la distribution est en effet une distribution (log-normale) de Pareto. Le plus minime problème sur la courbe2 indiquerait que les données ne suivent pas une distribution de Pareto. Nous devons nous rappeler que nous analysons une échelle Log-Log et que de petites variations sur le graphique représentent des rapports et non des différences absolues
Par exemple, une déviation de deux unités sur l’échelle signifie que nous avons deux fois la quantité ou la moitié de la quantité comparée à une distribution théorique de Pareto.
Une telle différence peut avoir diverses explications valables, c’est-à-dire que dans la distribution que nous observons, nous avons une situation spécifique se produisant à ce point précis de la courbe. Nous devrons alors rechercher les causes d’une telle déviation de la courbe à cet endroit.
Plus souvent, il s’agit d’un artefact, dû à notre méthodologie, qui déforme la distribution de manière « étrange ». Ceci peut être dû à un biais statistique lors du prélèvement de l’information (biais non détecté lors de la saisie des données, naturellement) ou d’une erreur dans l’approche d’extrapolation de l’échantillon, ou à n’importe quelle autre erreur de calcul.
Il se peut toutefois qu’une explication vienne confirmer la singularité de la forme de notre courbe : réglementation légales modifiant le comportement des agents économiques ou sociaux, effet de seuil, etc.
D’autres méthodes de test de validité peuvent être utilisées pour confirmer notre hypothèse avec des formules statistiques, par exemple le test du Chi Deux.
Je n’insisterai pas ici sur les méthodes de test de validité d’une hypothèse de distribution statistique.
Tracé d’une distribution de Pareto étapes par étape
Prenons par exemple la distribution des établissements par des classes de taille des employés aux Etats-Unis en 1970. (source : County Business Patterns, US Department of commerce)
Nous calculerons successivement la largeur de chaque classe de taille, de la valeur moyenne de chaque classe de taille des employés et des tailles de chaque barre correspondante d’histogramme.
Largeur de classe de taille
Pour chaque classe de taille, soustraire la valeur limite inférieure de la valeur limite supérieure et rajouter une unité. Cela nous rappelle les méchants problèmes d’intervalle ?…
Par exemple, si la classe de taille est de 5 à 9 employés, la largeur de la classe sera calculée de la façon suivante : (9 – 5) + 1 = 5
Taille moyenne par la classe de taille
Si possible quand les données la fournissent, il vaut mieux utiliser la moyenne réellement observée des tailles dans chacune des classes. Quand cette moyenne n’est pas fournie, on peut faire une estimation statistique faisant l’hypothèse que nous avons bien une distribution de Pareto ce que nous testerons ensuite bien évidemment. Pour chaque classe, il faut multiplier la valeur limite inférieure de taille par la valeur limite supérieure et calculer la racine carrée de ce produit (c’est ce qu’on appelle une moyenne géométrique).
Par exemple :
1 x 3 = 3
___
V 3 = 1,732 soit 1,7

Tailles de chaque barre d’histogramme de classe de taille
Pour chaque classe, divisez juste le nombre d’unités observées par la largeur de la classe de taille
Par exemple :1762340 : 3 = 587447.6

Tracé :
Nous pouvons maintenant tracer la courbe en reportant sur l’axe des Y les valeurs normalisées pour les populations observées dans chaque classe de tailles, et en utilisant sur l’axe des X la valeur moyenne géométrique de chaque classe de taille sur le papier Log-Log ou employer un programme de régression mathématique sur un ordinateur choisissant l’option Log-Log pour l’axe des X et l’axe des Y.


Second exemple :
Distribution des réseaux informatiques en fonction du le nombre de postes de travail connectés. Evaluations venant d’une première analyse conduite en Espagne.


L’aspect irrégulier de cette courbe, contrairement à ce qu’on attendrait d’une distribution Pareto / log-normale doit attirer notre attention et nous conduire à l’analyse de l’accident sur cette courbe.
Ce dernier pourrait être en effet très réel et être lié à une situation spécifique (effet de seuil, réglementation de normalisation ou limites techniques).
Dans la plupart des cas il doit cependant probablement être dû à de la polarisation dans notre technique échantillonnage (ce qui était le cas ici) ou à des erreurs de calcul.
Autres utilisations des distributions de Pareto :
Jusqu’ici nous avons seulement employé la distribution de Pareto pour examiner la forme d’une distribution que notre connaissance de l’environnement nous inciterait à assumer pour être de « type de Pareto ».
Interpolation à de nouvelles classes de taille :
Nous pouvons employer les propriétés de stabilité de ces distributions pour en déduire des informations non actuellement disponibles, par exemple pour comparer deux distributions pour lesquelles les limites de classe de taille ne sont pas identiques. Nous pouvons renverser la méthode de calcul précédente afin d’obtenir, à partir de la forme de la courbe, la valeur des quantités correspondant à une nouvelle classe de taille hypothétique.
Avant de faire que calcul en sens inverse, nous avons d’abord à calculer les coefficients de l’équation de la courbe. Pour cela nous employons un programme d’analyse de régression, dans ce cas-ci une régression du second degré. Ce programme doit être appliqué au logarithme des variables car c’est seulement dans un espace Log-Log que l’ajustement de la courbe à une équation polynomiale du second degré est appropriée.
REG2DEG (Log nombre d’entités ; Log moyenne Géométrique des classes ) ==> coefficients.
REG2DEG :
Nom de programme : employez celui disponible sur votre logiciel de statistiques
J’employais dans mon travail un programme que j’avais moi-même écrit avec le langage de programmation scientifique APL1 pour calculer les coefficients de régression parabolique
Les coefficients (COEF) sont les valeurs A B et C de l’équation :
Y = A X²+ B X + C
Dans laquelle grand X est le logarithme de la moyenne géométrique de la classe de taille.
Et grand Y est le logarithme de la valeur normalisée du nombre d’entités appartenant à la classe de taille X
Une fois que nous avons les coefficients, nous pouvons les employer dans l’équation du second degré pour calculer le logarithme de la valeur théorique normalisée pour la valeur moyenne géométriques interpolée de la nouvelle classe de tailles.
POLYNOM (Log de la nouvelle taille ; COEF)
POLYNOM :
Nom du Programme qui calcule de nouvelles valeurs en utilisant les coefficients précédents
A, B et C dans l’équation avec la nouvelle valeur moyenne X’ correspondent à la nouvelle classe de taille interpolée :
J’employais dans mon travail un autre programme APL pour extrapoler ou interpoler des valeurs théoriques à partir des coefficients de régression parabolique déterminés auparavant.
Y = A X’ ²+ B X’+ C
Dans laquelle grand X’ est le logarithme de la moyenne géométrique de la classe de taille interpolée.
Et grand Y’ est le logarithme de la valeur normalisée du nombre d’entités appartenant à la classe de taille X’ interpolée
APL est un langage de programmation destiné aux calculs et à la modélisation scientifique. La puissance de ce langage permet de résoudre des systèmes d’équations à n équations et p variables et donne une approximation selon la méthode de Jordan lorsque le nombre d’équation est supérieur au nombre de variables. C’est même une des fonctions de base du langage. Le langage contient aussi d’autres fonctions de bases telles que logarithmes, exponentielles et autres fonctions de grande utilité en analyse statistique.
La valeur réelle des tailles de barre d’histogramme peut alors être obtenue par l’élévation à une puissance de la base de logarithme, 10 en général, à la valeur calculée ci-dessus.
Quantité normalisée = 10 Y ‘
Rappelez-vous alors de multiplier la valeur théorique tirée de la courbe par la nouvelle largeur de classe de taille, afin obtenir la valeur absolue.
Quantité réelle = Quantité normalisée x largeur de la nouvelle classe
Cette méthode permet de recalculer des valeurs théoriques pour un ensemble de classes de tailles afin de pouvoir comparer des distributions obtenues à partir de sources différentes. Il peut être nécessaire d’effectuer une règle de trois sur les valeurs théoriques calculées afin d’arriver au même total exact que la population originale.
Extrapolation à de nouveaux environnements :
La distribution de Pareto est extrêmement fréquente et montre un degré élevé de robustesse. Elle peut être utilisée pour prévoir avec un degré de confidence assez élevée, l’évolution de certaines populations. Les coefficients des courbes sont très stables et leur variation, le cas échéant, reste très lente et monotone.
Si nous avons peu d’informations sur un pays, nous pouvons employer la distribution disponible pour la même population dans un autre pour lequel on dispose de meilleures statistiques, et en déduire, avec un degré de confidence assez élevée, une distribution par taille de certaines entités pour le pays pour lequel nous ne l’avions pas.
Conclusion
En résumé, l’analyse de distribution de Pareto est un outil puissant car elle permet à l’analyste d’examiner la validité générale d’une distribution observée et de se sentir confiant sur les quantités d’entités observées. Quand on trouve une déformation anormale de la courbe, c’est aussi une information importante qui nous dirige soit vers un domaine de recherche pour essayer de comprendre la raison véritable de la forme anormale de cette courbe, soit pour la correction d’une cause d’erreur qui avait été négligée dans l’étude.